解汉诺塔最常见的方法是递归法，记得上数据结构那门课的时候老师说过，递归法通常情况下都能够找到一种非递归的方法来实现，汉诺塔也有非递归的方法解决。

递归方法：

首先把三根柱子按顺序排成品字型，把所有的圆盘按从大到小的顺序放在柱子A上，根据圆盘的数量确定柱子的排放顺序：若n为偶数，按顺时针方向依次摆放 A B C；若n为奇数，按顺时针方向依次摆放 A C B。

1. 按顺时针方向把圆盘1从现在的柱子移动到下一根柱子，即当n为偶数时，若圆盘1在柱子A，则把它移动到B；若圆盘1在柱子B，则把它移动到C；若圆盘1在柱子C，则把它移动到A。
   

2. 接着，把另外两根柱子上可以移动的圆盘移动到新的柱子上。即把非空柱子上的圆盘移动到空柱子上，当两根柱子都非空时，移动较小的圆盘。这一步没有明确规定移动哪个圆盘，你可能以为会有多种可能性，其实不然，可实施的行动是唯一的。
   

3. 反复进行1、2操作，最后就能按规定完成汉诺塔的移动。
   

所以结果非常简单，就是按照移动规则向一个方向移动金片：
如3阶汉诺塔的移动：A→C,A→B,C→B,A→C,B→A,B→C,A→C

非递归方法：

1. 确定起点塔、终点塔，确定层数n

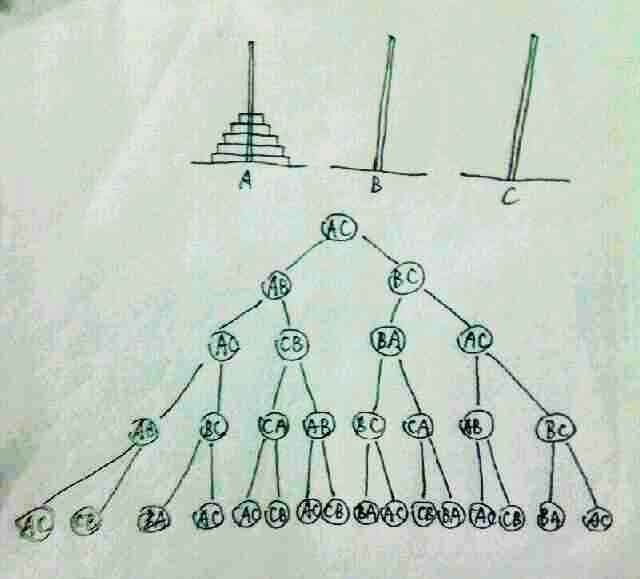
2. 若由A到C，画出其下分支

                    A→C                          1

           A→B          B→C                  2

   A→C   C→B    B→A   A→C           3

3. 中序遍历得到结果：A→C, A→B, C→B, A→C, B→A , B→C, A→C

5阶汉诺塔二叉树(演算手稿)

这种非递归的方法在手工演算方面着实简易，只需列出这棵二叉树便能够迅速写出答案。哈哈，挺适合做试卷的。不过，用此方法编程从理解上到也是比较容易的，比起递归法可能代码稍多但理解较易。